第 1 章入门介绍

本书中所有的数据分析我们都使用R语言。我们假设你有基础的编程能力和R语言语法的知识。如果你没有这些基础知识，你第一个要做的就是学习R的基础知识。这里我们会从安装R开始一步一步的教你如何使用R。

1.1 安装R

第一步是安装R。你可以从R的官网上下载R。安装的过程非常简单，但是如果你需要更多的帮助，你可以下载下面对应的资源。

下面的一步是安装Rstudio。Rstudio。在不安装Rstudio的情况下，你可以运行本书中所有的R代码，但是我们强烈推荐使用Rstudio这款集成开发环境软件。具体的下载链接见这里(http://www.rstudio.com/products/rstudio/download/)。对于Windows系统，我们也有一个对应的安装手册：https://github.com/genomicsclass/windows.

1.2 R基础知识

你首先要做的是让你自己对R编程和R的语法熟悉起来，你可以通过完成一个R的基本教程来实现这个目的。为了能够理解本书，你需要理解列表（list），数值向量（numeric vectors），能够写函数，以及理解如何使用sapply和replicate这两个函数。

如果你已经对R非常熟悉，你可以跳过下一节。如果你不熟悉，我们建议你完成swirl教程，这个教程会以交互的方式教你R编程和数字科学。在你安装R后，你可以安装swirl，然后以下面的方式运行它：

install.packages("swirl")
library(swirl)
swirl()

你也可以尝试Code School的try R课程。

&emsp&emsp同时，你也可以找到许多学习R的开源的资源和手册。这里我们给出两个例子：

R快速入门（Quick-R）: a quick online reference for data input, basic statistics and plots
R参考卡（R reference card） (PDF)[https://cran.r-project.org/doc/contrib/Short-refcard.pdf] by Tom Short

&emsp&emsp关于R有两个关键的内容：一是你能够使用 help``?

?install.packages
help("install.packages")

&emsp&emsp另一个就是#号表示注释，#号后面的内容是不会执行的。注释对编程代码的可读性是非常重要的。良好的注释是优秀代码的主要组成部分。

##This is just a comment

1.3 Installing Packages

The first R command we will run is install.packages. If you took the swirl tutorial you should have already done this. R only includes a basic set of functions. It can do much more than this, but not everybody needs everything so we instead make some functions available via packages. Many of these functions are stored in CRAN. Note that these packages are vetted: they are checked for common errors and they must have a dedicated maintainer. You can easily install packages from within R if you know the name of the packages. As an example, we are going to install the package rafalib which we use in our first data analysis examples:

install.packages("rafalib")

We can then load the package into our R sessions using the library function:

library(rafalib)

From now on you will see that we sometimes load packages without installing them. This is because once you install the package, it remains in place and only needs to be loaded with library. If you try to load a package and get an error, it probably means you need to install it first.

1.4 Importing Data into R

The first step when preparing to analyze data is to read in the data into R. There are several ways to do this and we will discuss three of them. But you only need to learn one to follow along.

In the life sciences, small datasets such as the one used as an example in the next sections are typically stored as Excel files. Although there are R packages designed to read Excel (xls) format, you generally want to avoid this and save files as comma delimited (Comma-Separated Value/CSV) or tab delimited (Tab-Separated Value/TSV/TXT) files. These plain-text formats are often easier for sharing data with collaborators, as commercial software is not required for viewing or working with the data. We will start with a simple example dataset containing female mouse weights.

第一步是找到对应的文件并且弄清楚这个文件的路径。

1.4.0.1 路径和工作目录

当你在

getwd()

You can also change your working directory using the function setwd. Or you can change it through RStudio by clicking on “Session”.

The functions that read and write files (there are several in R) assume you mean to look for files or write files in the working directory. Our recommended approach for beginners will have you reading and writing to the working directory. However, you can also type the full path, which will work independently of the working directory.

1.4.0.2 Projects in RStudio

We find that the simplest way to organize yourself is to start a Project in RStudio (Click on “File” and “New Project”). When creating the project, you will select a folder to be associated with it. You can then download all your data into this folder. Your working directory will be this folder.

1.4.0.3 Option 1: Read file over the Internet

You can navigate to the femaleMiceWeights.csv file by visiting the data directory of dagdata on GitHub. If you navigate to the file, you need to click on Raw on the upper right hand corner of the page.

GitHub page screenshot.

Now you can copy and paste the URL and use this as the argument to read.csv. Here we break the URL into a base directory and a filename and then combine with paste0 because the URL would otherwise be too long for the page. We use paste0 because we want to put the strings together as is, if you were specifying a file on your machine you should use the smarter function, file.path, which knows the difference between Windows and Mac file path connectors. You can specify the URL using a single string to avoid this extra step.

dir <- "https://raw.githubusercontent.com/genomicsclass/dagdata/master/inst/extdata/"
url <- paste0(dir, "femaleMiceWeights.csv")
dat <- read.csv(url)

1.4.0.4 Option 2: Download file with your browser to your working directory

There are reasons for wanting to keep a local copy of the file. For example, you may want to run the analysis while not connected to the Internet or you may want to ensure reproducibility regardless of the file being available on the original site. To download the file, as in option 1, you can navigate to the femaleMiceWeights.csv. In this option we use your browser’s “Save As” function to ensure that the downloaded file is in a CSV format. Some browsers add an extra suffix to your filename by default. You do not want this. You want your file to be named femaleMiceWeights.csv. Once you have this file in your working directory, then you can simply read it in like this:

dat <- read.csv("femaleMiceWeights.csv")

If you did not receive any message, then you probably read in the file successfully.

1.4.0.5 Option 3: Download the file from within R

We store many of the datasets used here on GitHub. You can save these files directly from the Internet to your computer using R. In this example, we are using the download.file function in the downloader package to download the file to a specific location and then read it in. We can assign it a random name and a random directory using the function tempfile, but you can also save it in directory with the name of your choosing.

library(downloader) ##use install.packages to install
dir <- "https://raw.githubusercontent.com/genomicsclass/dagdata/master/inst/extdata/"
filename <- "femaleMiceWeights.csv" 
url <- paste0(dir, filename)
if (!file.exists(filename)) download(url, destfile=filename)

We can then proceed as in option 2:

dat <- read.csv(filename)

1.4.0.6 Option 4: Download the data package (Advanced)

Many of the datasets we include in this book are available in custom-built packages from GitHub. The reason we use GitHub, rather than CRAN, is that on GitHub we do not have to vet packages, which gives us much more flexibility.

To install packages from GitHub you will need to install the devtools package:

install.packages("devtools")

Note to Windows users: to use devtools you will have to also install Rtools. In general you will need to install packages as administrator. One way to do this is to start R as administrator. If you do not have permission to do this, then it is a bit more complicated.

Now you are ready to install a package from GitHub. For this we use a different function:

library(devtools)
install_github("genomicsclass/dagdata")

The file we are working with is actually included in this package. Once you install the package, the file is on your computer. However, finding it requires advanced knowledge. Here are the lines of code:

dir <- system.file(package="dagdata") #extracts the location of package
list.files(dir)

## [1] "data"        "DESCRIPTION" "extdata"    
## [4] "help"        "html"        "Meta"       
## [7] "NAMESPACE"   "script"

list.files(file.path(dir,"extdata")) #external data is in this directory

## [1] "admissions.csv"              
## [2] "astronomicalunit.csv"        
## [3] "babies.txt"                  
## [4] "femaleControlsPopulation.csv"
## [5] "femaleMiceWeights.csv"       
## [6] "mice_pheno.csv"              
## [7] "msleep_ggplot2.csv"          
## [8] "README"                      
## [9] "spider_wolff_gorb_2013.csv"

And now we are ready to read in the file:

filename <- file.path(dir,"extdata/femaleMiceWeights.csv")
dat <- read.csv(filename)

1.4.1 Getting Started Exercises

Exercises

Here we will test some of the basics of R data manipulation which you should know or should have learned by following the tutorials above. You will need to have the file femaleMiceWeights.csv in your working directory. As we showed above, one way to do this is by using the downloader package:

library(downloader) 
url <- "https://raw.githubusercontent.com/genomicsclass/dagdata/master/inst/extdata/femaleMiceWeights.csv"
filename <- "femaleMiceWeights.csv" 
download(url, destfile=filename)

Read in the file femaleMiceWeights.csv and report the body weight of the mouse in the exact name of the column containing the weights.
The [ and ] symbols can be used to extract specific rows and specific columns of the table. What is the entry in the 12th row and second column?
You should have learned how to use the $ character to extract a column from a table and return it as a vector. Use $ to extract the weight column and report the weight of the mouse in the 11th row.
The length function returns the number of elements in a vector. How many mice are included in our dataset?
To create a vector with the numbers 3 to 7, we can use seq(3,7) or, because they are consecutive, 3:7. View the data and determine what rows are associated with the high fat or hf diet. Then use the mean function to compute the average weight of these mice.
One of the functions we will be using often is sample. Read the help file for sample using ?sample. Now take a random sample of size 1 from the numbers 13 to 24 and report back the weight of the mouse represented by that row. Make sure to type set.seed(1) to ensure that everybody gets the same answer.

1.5 Brief Introduction to `dplyr`

The learning curve for R syntax is slow. One of the more difficult aspects that requires some getting used to is subsetting data tables. The dplyr package brings these tasks closer to English and we are therefore going to introduce two simple functions: one is used to subset and the other to select columns.

Take a look at the dataset we read in:

filename <- "femaleMiceWeights.csv"
dat <- read.csv(filename)
head(dat) #In R Studio use View(dat)

##   Diet Bodyweight
## 1 chow      21.51
## 2 chow      28.14
## 3 chow      24.04
## 4 chow      23.45
## 5 chow      23.68
## 6 chow      19.79

There are two types of diets, which are denoted in the first column. If we want just the weights, we only need the second column. So if we want the weights for mice on the chow diet, we subset and filter like this:

library(dplyr) 
chow <- filter(dat, Diet=="chow") #keep only the ones with chow diet
head(chow)

##   Diet Bodyweight
## 1 chow      21.51
## 2 chow      28.14
## 3 chow      24.04
## 4 chow      23.45
## 5 chow      23.68
## 6 chow      19.79

And now we can select only the column with the values:

chowVals <- select(chow,Bodyweight)
head(chowVals)

##   Bodyweight
## 1      21.51
## 2      28.14
## 3      24.04
## 4      23.45
## 5      23.68
## 6      19.79

A nice feature of the dplyr package is that you can perform consecutive tasks by using what is called a “pipe”. In dplyr we use %>% to denote a pipe. This symbol tells the program to first do one thing and then do something else to the result of the first. Hence, we can perform several data manipulations in one line. For example:

chowVals <- filter(dat, Diet=="chow") %>% select(Bodyweight)

In the second task, we no longer have to specify the object we are editing since it is whatever comes from the previous call.

Also, note that if dplyr receives a data.frame it will return a data.frame.

class(dat)

## [1] "data.frame"

class(chowVals)

## [1] "data.frame"

For pedagogical reasons, we will often want the final result to be a simple numeric vector. To obtain such a vector with dplyr, we can apply the unlist function which turns lists, such as data.frames, into numeric vectors:

chowVals <- filter(dat, Diet=="chow") %>% select(Bodyweight) %>% unlist
class( chowVals )

## [1] "numeric"

To do this in R without dplyr the code is the following:

chowVals <- dat[ dat$Diet=="chow", colnames(dat)=="Bodyweight"]

1.5.1 `dplyr` exercises

Exercises

For these exercises, we will use a new dataset related to mammalian sleep. This data is described here. Download the CSV file from this location:

We are going to read in this data, then test your knowledge of they key dplyr functions select and filter. We are also going to review two different classes: data frames and vectors.

Read in the msleep_ggplot2.csv file with the function read.csv and use the function class to determine what type of object is returned.
Now use the filter function to select only the primates. How many animals in the table are primates? Hint: the nrow function gives you the number of rows of a data frame or matrix.
What is the class of the object you obtain after subsetting the table to only include primates?
Now use the select function to extract the sleep (total) for the primates. What class is this object? Hint: use %>% to pipe the results of the filter function to select.
Now we want to calculate the average amount of sleep for primates (the average of the numbers computed above). One challenge is that the mean function requires a vector so, if we simply apply it to the output above, we get an error. Look at the help file for unlist and use it to compute the desired average.
For the last exercise, we could also use the dplyr summarize function. We have not introduced this function, but you can read the help file and repeat exercise 5, this time using just filter and summarize to get the answer.

1.6 Mathematical Notation

This book focuses on teaching statistical concepts and data analysis programming skills. We avoid mathematical notation as much as possible, but we do use it. We do not want readers to be intimidated by the notation though. Mathematics is actually the easier part of learning statistics. Unfortunately, many text books use mathematical notation in what we believe to be an over-complicated way. For this reason, we do try to keep the notation as simple as possible. However, we do not want to water down the material, and some mathematical notation facilitates a deeper understanding of the concepts. Here we describe a few specific symbols that we use often. If they appear intimidating to you, please take some time to read this section carefully as they are actually simpler than they seem. Because by now you should be somewhat familiar with R, we will make the connection between mathematical notation and R code.

1.6.0.1 Indexing

Those of us dealing with data almost always have a series of numbers. To describe the concepts in an abstract way, we use indexing. For example 5 numbers:

x <- 1:5

can be generally represented like this $x_1, x_2, x_3, x_4, x_5$. We use dots to simplify this $x_1,\dots,x_5$ and indexing to simplify even more $x_i, i=1,\dots,5$. If we want to describe a procedure for a list of any size $n$, we write $x_i, i=1,\dots,n$.

We sometimes have two indexes. For example, we may have several measurements (blood pressure, weight, height, age, cholesterol level) for 100 individuals. We can then use double indexes: $x_{i,j}, i=1,\dots,100, j=1,\dots,5$.

1.6.0.2 Summation

A very common operation in data analysis is to sum several numbers. This comes up, for example, when we compute averages and standard deviations. If we have many numbers, there is a mathematical notation that makes it quite easy to express the following:

n <- 1000
x <- 1:n
S <- sum(x)

and it is the $\sum$ notation (capital S in Greek):

\[ S = \sum_{i=1}^n x_i \]

Note that we make use of indexing as well. We will see that what is included inside the summation can become quite complicated. However, the summation part should not confuse you as it is a simple operation.

1.6.0.3 Greek letters

We would prefer to avoid Greek letters, but they are ubiquitous in the statistical literature so we want you to become used to them. They are mainly used to distinguish the unknown from the observed. Suppose we want to find out the average height of a population and we take a sample of 1,000 people to estimate this. The unknown average we want to estimate is often denoted with $\mu$, the Greek letter for m (m is for mean). The standard deviation is often denoted with $\sigma$, the Greek letter for s. Measurement error or other unexplained random variability is typically denoted with $\varepsilon$, the Greek letter for e. Effect sizes, for example the effect of a diet on weight, are typically denoted with $\beta$. We may use other Greek letters but those are the most commonly used.

You should get used to these four Greek letters as you will be seeing them often: $\mu$, $\sigma$, $\beta$ and $\varepsilon$.

Note that indexing is sometimes used in conjunction with Greek letters to denote different groups. For example, if we have one set of numbers denoted with $x$ and another with $y$ we may use $\mu_x$ and $\mu_y$ to denote their averages.

1.6.0.4 Infinity

In the text we often talk about asymptotic results. Typically, this refers to an approximation that gets better and better as the number of data points we consider gets larger and larger, with perfect approximations occurring when the number of data points is $\infty$. In practice, there is no such thing as $\infty$, but it is a convenient concept to understand. One way to think about asymptotic results is as results that become better and better as some number increases and we can pick a number so that a computer can’t tell the difference between the approximation and the real number. Here is a very simple example that approximates 1/3 with decimals:

onethird <- function(n) sum( 3/10^c(1:n))
1/3 - onethird(4)

## [1] 3.333e-05

1/3 - onethird(10)

## [1] 3.333e-11

1/3 - onethird(16)

## [1] 0

In the example above, 16 is practically $\infty$.

1.6.0.5 Integrals

We only use these a couple of times so you can skip this section if you prefer. However, integrals are actually much simpler to understand than perhaps you realize.

For certain statistical operations, we need to figure out areas under the curve. For example, for a function $f(x)$ …

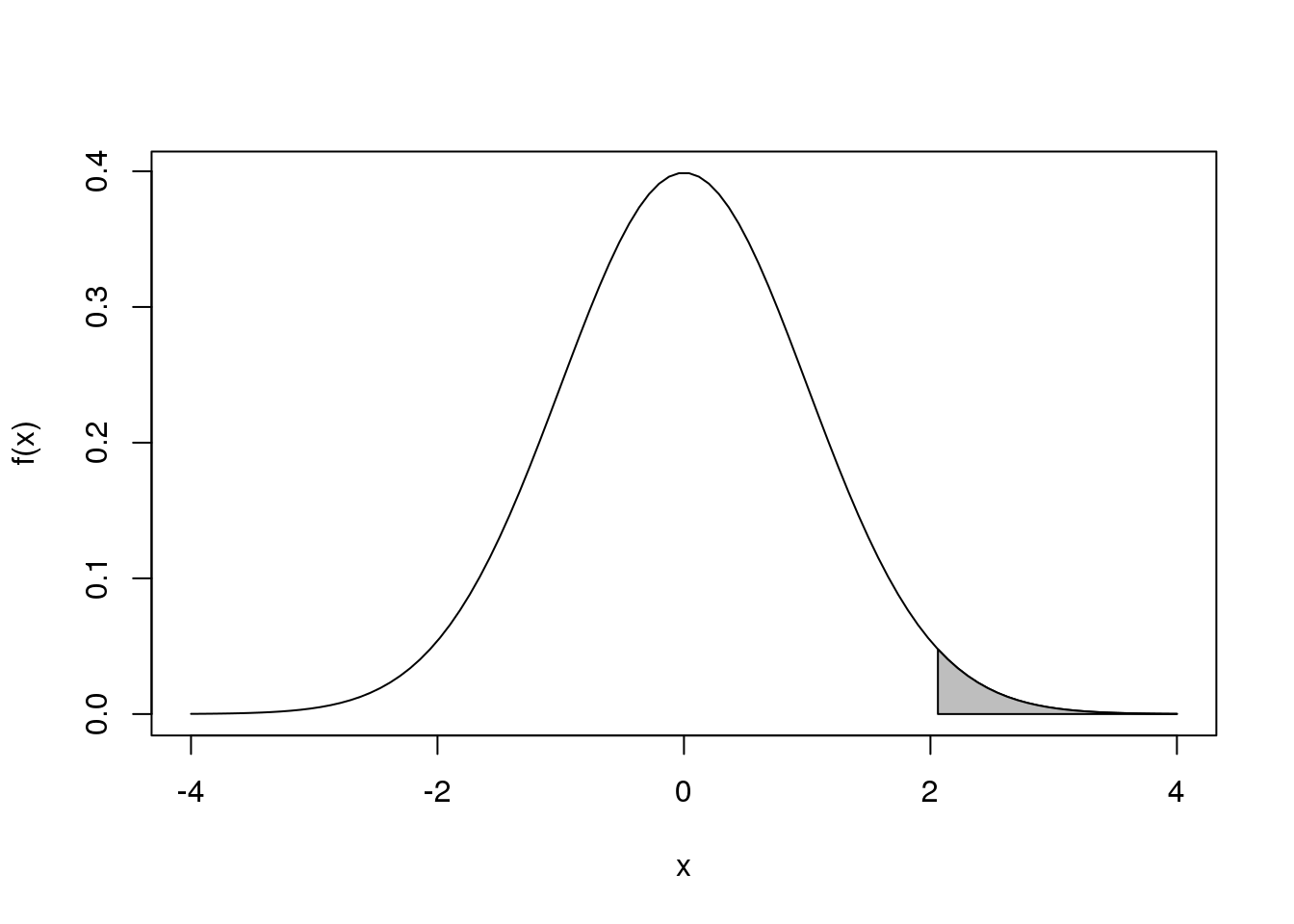
图 1.1: Integral of a function.

…we need to know what proportion of the total area under the curve is grey.

The grey area can be thought of as many small grey bars stacked next to each other. The area is then just the sum of the areas of these little bars. The problem is that we can’t do this for every number between 2 and 4 because there are an infinite number. The integral is the mathematical solution to this problem. In this case, the total area is 1 so the answer to what proportion is grey is the following integral:

\[ \int_2^4 f(x) \, dx \]

Because we constructed this example, we know that the grey area is 2.27% of the total. Note that this is very well approximated by an actual sum of little bars:

width <- 0.01
x <- seq(2,4,width)
areaofbars <-  f(x)*width
sum( areaofbars )

## [1] 0.02299

The smaller we make width, the closer the sum gets to the integral, which is equal to the area.

第 1 章 入门介绍